Finanzmathematik
Finanzmathematik - Definition
Zweig der Mathematik, der sich mit finanzwirtschaftlichen Entscheidungsproblemen, z. B. der Berechnung von Zinsen, Tilgung, Renten, Annuitäten und Bar- bzw. Kapitalwerten, beschäftigt. Die finanzmathematischen Grundformeln sind im Folgenden zusammengefasst und werden jeweils mit einem kurzen Beispiel erläutert.
Gliederung
100 € sollen für 2 Jahre bei einem Zinssatz von 10 % angelegt werden. Den Anleger interessiert der Endwert.
Kapital am Ende des 1. Jahres:
100 + (0,1 × 100) = 110
Kapital am Ende des 2. Jahres:
100 + (0,1 × 100) + 0,1 (100 + 0,1 = 100)
= 100 (1 + 0,1) + 0,1 (100[1 + 0,1])
= 100< (1 + 0,1) × (1 + 0,1)
= 100 (1 + 0,1)2
= 121 €
Aufzinsungsfaktor: (1 + i)n
i = Zinssatz, n = Anlagezeitraum, Nutzungsdauer
121 € werden in 2 Jahren benötigt. Der Zinssatz betrage 10 %. Den Sparer interessiert seine notwendige Spareinlage heute, um zusammen mit den Zinsen in zwei Jahren 121 € zur Verfügung zu haben.
Kapitaleinsatz heute:
K + (0,1 K) + 0,1 (K + 0,1 K) = 121
K = (1 + 0,1)2 = 121
K = 121/(1 + 0,1)2
K = 100 €
Abzinsungsfaktor: 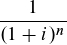
Eine Rente von 100,- € soll drei Jahre lang jeweils am Ende eines jeden Jahres ausbezahlt werden. Den Sparer interessiert der heutige Wert seiner dreijährigen Rentenzahlung, d. h. der abgezinste Wert seiner gleichbleibenden Zahlungsreihe. Er rechnet mit einem Wertverlust des Geldes von 10% pro Jahr (Abzinsung mit i = 0,1)
Abzinsung:
100 (1/[1 + i]1) + 100 (1/[1 + i]2) + 100 (1/[1 + i]3
90,90 + 82,64 + 75,13 = 248,67 €
Daraus ist der Rentenbarwertfaktor ableitbar:
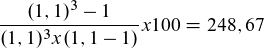
Rentenbarwertfaktor:
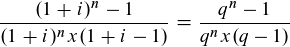
Ein Kapital von 248,67 €, das heute zur Verfügung steht, soll zu einem Zinssatz von 10% angelegt und in den nächsten drei Jahren als Rente in gleichhohen Beträgen, jeweils am Ende eines Jahres, ausbezahlt werden.
Gleichsetzung des Kapitals mit den abgezinsten gleichhohen Rentenbeträgen der 3 Jahre
248,67 € = R (1/[1 + i]1) + R (1/[1 + i]2) + R (1/[1 + i]3) R = 100
Daraus ist ein Wiedergewinnungsfaktor ableitbar:
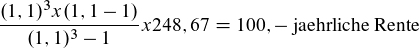
Wiedergewinnungsfaktor:
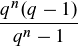
Unterjährige Verzinsung bei Wiederanlage von Zinsen zum aktuellen Zinssatz
▪ 100 € waren zwei Jahre lang angelegt, wobei Zinsen quartalsweise, also viermal jährlich gezahlt wurden.
▪ Barwert = 100 x 1/(1 + 0,1/4)4 x 1 + 100 x 1/(1 + 0,1/4)4 x 2 = 235,88
▪ Endwert = 100 (1 + 0,1/4)4 x 1 + 100 (1 + 0,1/4)4 x 2 = 251,76
Abzinsungsfaktor bei unterjähriger Verzinsung: 1/(1 + i/m)mn
Aufzinsungsfaktor bei unterjähriger Verzinsung: (1 + i/m)mn
m = Anzahl der Zinstermine pro Jahr
Ähnliche Begriffe und Ergebnisse
In Kategorien
Für wissenschaftliche Arbeiten
Quelle & Zitierlink
Um diese Seite in einer wissenschaftlichen Arbeit als Quelle anzugeben, können Sie folgenden Link verwenden, um sicherzustellen, dass sich der Inhalt des Artikels nicht ändert.

